Using Generated Keys For Encryption Rsa C++
Chilkat • HOME • Android™ • Classic ASP • C • C++ • C# • Mono C# • .NET Core C# • C# UWP/WinRT • DataFlex • Delphi ActiveX • Delphi DLL • Visual FoxPro • Java • Lianja • MFC • Objective-C • Perl • PHP ActiveX • PHP Extension • PowerBuilder • PowerShell • PureBasic • CkPython • Chilkat2-Python • Ruby • SQL Server • Swift 2 • Swift 3/4 • Tcl • Unicode C • Unicode C++ • Visual Basic 6.0 • VB.NET • VB.NET UWP/WinRT • VBScript • Xojo Plugin • Node.js • Excel • Go
| C sample code to RSA public-key encrypt and decrypt strings using public and private keys.
| |||||
© 2000-2020 Chilkat Software, Inc. All Rights Reserved.

Rsa Encryption History
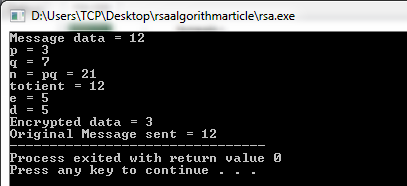
Using Generated Keys For Encryption Rsa C File
Mar 15, 2012 Demonstration of using OpenSSL to create RSA public/private key pair, sign and encrypt messages using those keys and then decrypt and verify the received messages. Commands used: openssl. Generating Keys for Encryption and Decryption.; 3 minutes to read +7; In this article. Creating and managing keys is an important part of the cryptographic process. Symmetric algorithms require the creation of a key and an initialization vector (IV). The key must be kept secret from anyone who should not decrypt your data. RSA (Rivest–Shamir–Adleman) is an algorithm used by modern computers to encrypt and decrypt messages. It is an asymmetric cryptographic algorithm. Asymmetric means that there are two different keys.This is also called public key cryptography, because one of the keys can be given to anyone.The other key must be kept private. I'm looking for a C/C implementation of RSA with a 2048 bit key (preferably read from a file). My target is an embedded platform, so it comes with some odd restrictions. The hardware restricts us from using the new operator, and we have to use a special version of malloc supplied by the hardware manufacturer called 'umalloc'. First of all, you cannot use a private key for signing and encryption, you'd use it for signing and decryption. In PKI/TLS/SSL asymmetric encryption is not used to transmit the public key when RSA session key agreement is used. The public key is within a (signed) certificate, the private key stays at the server. Now, since RSA keys are so large (often 1024 bits and above), the primes have to be at least half that (at least 512 bits then). Such large primes would be difficult to generate (you'd have to check many, many numbers and try to factor each of them), so I understand that the typical approach is to use pre-generated lists of large primes.
