Hash Generation Requires Secret Key

14.04.2020 admin

ntv.netlify.com › ► ► Hash Generation Requires Secret Key ► ►

DBMS_CRYPTO provides an interface to encrypt and decrypt stored data, and can be used in conjunction with PL/SQL programs running network communications. It provides support for several industry-standard encryption and hashing algorithms, including the Advanced Encryption Standard (AES) encryption algorithm. AES has been approved by the National Institute of Standards and Technology (NIST) to replace the Data Encryption Standard (DES).

Hash Generation Requires Secret Key West
Hash Generation Requires Secret Key Movie

HMAC uses two passes of hash computation. The secret key is first used to derive two keys – inner and outer. The first pass of the algorithm produces an internal hash derived from the message and the inner key. The second pass produces the final HMAC code derived from the inner hash result and the outer key. Thus the algorithm provides better immunity against length extension attacks.

A keyed-hash message authentication code (HMAC) uses a cryptographic hash function (MD5, SHA-1, SHA-512 ) and a secret cryptographic key to verify both the data integrity and the authentication of a message.
This online hash generator converts your sensitive data like passwords to a SHA-1 hash. To calculate a checksum of a file, you can use the upload feature. For further security of the encryption process you can define a HMAC key.
The HASH function included with DBMSCRYPTO, is a one-way hash function that you can use to generate a hash value from either RAW or LOB data. The MAC function is also a one-way hash function, but with the addition of a secret key.

Using the DBMS_CRYPTO Subprograms

Overview

DBMS_CRYPTO contains basic cryptographic functions and procedures. To use this package correctly and securely, a general level of security expertise is assumed.

The DBMS_CRYPTO package enables encryption and decryption for common Oracle datatypes, including RAW and large objects (LOBs), such as images and sound. Specifically, it supports BLOBs and CLOBs. In addition, it provides Globalization Support for encrypting data across different database character sets.

The following cryptographic algorithms are supported:

Data Encryption Standard (DES), Triple DES (3DES, 2-key and 3-key)
Advanced Encryption Standard (AES)
MD5, MD4, SHA-1, and SHA-2 cryptographic hashes
MD5, SHA-1, and SHA-2 Message Authentication Code (MAC)

Block cipher modifiers are also provided with DBMS_CRYPTO. You can choose from several padding options, including PKCS (Public Key Cryptographic Standard) #5, and from four block cipher chaining modes, including Cipher Block Chaining (CBC).

Table 40-1 summarizes the DBMS_CRYPTO package features.

Table 40-1 DBMS_CRYPTO Features

Package Feature	DBMS_CRYPTO
Cryptographic algorithms	DES, 3DES, AES, RC4, 3DES_2KEY
Padding forms	PKCS5, zeroes
Block cipher chaining modes	CBC, CFB, ECB, OFB
Cryptographic hash algorithms	MD5, SHA-1, SHA-2 (SHA-256, SHA-384, SHA-512), MD4
Keyed hash (MAC) algorithms	HMAC_MD5, HMAC_SH1, HMAC_SH256, HMAC_SH384, HMAC_SH512
Cryptographic pseudo-random number generator	`RAW`, `NUMBER`, `BINARY_INTEGER`
Database types	`RAW`, `CLOB`, `BLOB`

The DBMS_CRYPTO package replaces DBMS_OBFUSCATION_TOOLKIT, providing greater ease of use and support for a range of algorithms to accommodate new and existing systems. Specifically, 3DES_2KEY and MD4 are provided for backward compatibility. It is not recommended that you use these algorithms because they do not provide the same level of security as provided by 3DES, AES, MD5, SHA-1, or SHA-2.

Security Model

Oracle Database installs this package in the SYS schema. You can then grant package access to existing users and roles as needed.

Datatypes

Parameters for the DBMS_CRYPTO subprograms use these datatypes:

Table 40-2 DBMS_CRYPTO Datatypes

Type	Description
`BLOB`	A source or destination binary LOB
`CLOB`	A source or destination character LOB (excluding NCLOB)
`PLS_INTEGER`	Specifies a cryptographic algorithm type (used with BLOB, CLOB, and RAW datatypes)
`RAW`	A source or destination RAW buffer Find all the serial numbers we have in our database for: genesis generation x2. Even more serial numbers might be present in our database for this title. New serials are added on daily bases to cover new releases of the this application. Search next days to see new results. The GenX2 product includes support for the DAZ generation 4 figures and Genesis as sources for morph transfers and for Genesis as target. Further figures are supported by separate add-ons. To transfer morphs from or to Genesis 2 Male or Female, the GenX2 AddOn for Genesis 2 is required. Jul 24, 2019 3 and 8 Female(s) and Genesis 3 Auto Rickshaw Character and Hair Bundle Christmas Tree Clothing and Hair Bundle Everyday items FashionDress 3 for Genesis 3 Females G2F G2M G3 G3 and V7 G3F G3M and M7 Genesis 2 Genesis 2 Female(s) and V4 Genesis 2 Female(s) and Victoria 4 Genesis 8 Male and Michael 8 Hair i13 Complex Variety Pose Collection for. Genesis Generation X2 Serial Numbers. Convert Genesis Generation X2 trail version to full software.

Algorithms

The following cryptographic algorithms, modifiers, and cipher suites are predefined in this package.

Table 40-3 DBMS_CRYPTO Cryptographic Hash Functions

Name	Description
`HASH_MD4`	Produces a 128-bit hash, or message digest of the input message
`HASH_MD5`	Also produces a 128-bit hash, but is more complex than MD4
`HASH_SH1`	Secure Hash Algorithm (SHA-1). Produces a 160-bit hash.
`HASH_SH256`	SHA-2, produces a 256-bit hash.
`HASH_SH384`	SHA-2, produces a 384-bit hash.
`HASH_SH512`	SHA-2, produces a 512-bit hash.

Table 40-4 DBMS_CRYPTO MAC (Message Authentication Code) Functions

Name	Description
`HMAC_MD5`^{Foot 1}	Same as MD5 hash function, except it requires a secret key to verify the hash value.
`HMAC_SH1`^{Footref 1}	Same as SHA hash function, except it requires a secret key to verify the hash value.
`HMAC_SH256`	Same as SHA-2 256-bit hash function, except it requires a secret key to verify the hash value.
`HMAC_SH384`	Same as SHA-2 384-bit hash function, except it requires a secret key to verify the hash value.
`HMAC_SH512`	Same as SHA-2 512-bit hash function, except it requires a secret key to verify the hash value.

^{Footnote 1}Complies with IETF RFC 2104 standard

Table 40-5 DBMS_CRYPTO Encryption Algorithms

Name	Description
`ENCRYPT_DES`	Data Encryption Standard. Block cipher. Uses key length of 56 bits.
`ENCRYPT_3DES_2KEY`	Data Encryption Standard. Block cipher. Operates on a block 3 times with 2 keys. Effective key length of 112 bits.
`ENCRYPT_3DES`	Data Encryption Standard. Block cipher. Operates on a block 3 times.
`ENCRYPT_AES128`	Advanced Encryption Standard. Block cipher. Uses 128-bit key size.
`ENCRYPT_AES192`	Advanced Encryption Standard. Block cipher. Uses 192-bit key size.
`ENCRYPT_AES256`	Advanced Encryption Standard. Block cipher. Uses 256-bit key size.
`ENCRYPT_RC4`	Stream cipher. Uses a secret, randomly generated key unique to each session.

Table 40-6 DBMS_CRYPTO Block Cipher Suites

Name	Description
`DES_CBC_PKCS5`	ENCRYPT_DES^{Foot 1} + CHAIN_CBC^{Foot 2}+ PAD_PKCS5^{Foot 3}
`DES3_CBC_PKCS5`	`ENCRYPT_3DES`^{Footref 1} + `CHAIN_CBC`^{Footref 2} + PAD_PKCS5^{Footref 3}

^{Footnote 1}See Table 40-5, 'DBMS_CRYPTO Encryption Algorithms'

^{Footnote 2}See Table 40-7, 'DBMS_CRYPTO Block Cipher Chaining Modifiers'

^{Footnote 3}See Table 40-8, 'DBMS_CRYPTO Block Cipher Padding Modifiers'

Table 40-7 DBMS_CRYPTO Block Cipher Chaining Modifiers

Name	Description
`CHAIN_ECB`	Electronic Codebook. Encrypts each plaintext block independently.
`CHAIN_CBC`	Cipher Block Chaining. Plaintext is XORed with the previous ciphertext block before it is encrypted.
`CHAIN_CFB`	Cipher-Feedback. Enables encrypting units of data smaller than the block size.
`CHAIN_OFB`	Output-Feedback. Enables running a block cipher as a synchronous stream cipher. Similar to CFB, except that n bits of the previous output block are moved into the right-most positions of the data queue waiting to be encrypted.

Table 40-8 DBMS_CRYPTO Block Cipher Padding Modifiers

Name	Description
`PAD_PKCS5`	Provides padding which complies with the PKCS #5: Password-Based Cryptography Standard
`PAD_NONE`	Provides option to specify no padding. Caller must ensure that blocksize is correct, else the package returns an error.
`PAD_ZERO`	Provides padding consisting of zeroes

Restrictions

The VARCHAR2 datatype is not directly supported by DBMS_CRYPTO. Before you can perform cryptographic operations on data of the type VARCHAR2, you must convert it to the uniform database character set AL32UTF8, and then convert it to the RAW datatype. After performing these conversions, you can then encrypt it with the DBMS_CRYPTO package.

Exceptions

Table 40-9 lists exceptions that have been defined for DBMS_CRYPTO.

Table 40-9 DBMS_CRYPTO Exceptions

Exception	Code	Description
`CipherSuiteInvalid`	`28827`	The specified cipher suite is not defined.
`CipherSuiteNull`	`28829`	No value has been specified for the cipher suite to be used.
`KeyNull`	`28239`	The encryption key has not been specified or contains a `NULL` value.
`KeyBadSize`	`28234`	DES keys: Specified key size is too short. DES keys must be at least 8 bytes (64 bits). AES keys: Specified key size is not supported. AES keys must be 128, 192, or 256 bits in length.
`DoubleEncryption`	`28233`	Source data was previously encrypted.

Operational Notes

When to Use Encrypt and Decrypt Procedures or Functions

This package includes both ENCRYPT and DECRYPT procedures and functions. The procedures are used to encrypt or decrypt LOB datatypes (overloaded for CLOB and BLOB datatypes). In contrast, the ENCRYPT and DECRYPT functions are used to encrypt and decrypt RAW datatypes. Data of type VARCHAR2 must be converted to RAW before you can use DBMS_CRYPTO functions to encrypt it.

When to Use Hash or Message Authentication Code (MAC) Functions

This package includes two different types of one-way hash functions: the HASH function and the MAC function. Hash functions operate on an arbitrary-length input message, and return a fixed-length hash value. One-way hash functions work in one direction only. It is easy to compute a hash value from an input message, but it is extremely difficult to generate an input message that hashes to a particular value. Note that hash values should be at least 128 bits in length to be considered secure.

You can use hash values to verify whether data has been altered. For example, before storing data, the user runs DBMS_CRYPTO.HASH against the stored data to create a hash value. On returning the stored data, the user can again run the hash function against it, using the same algorithm. If the second hash value is identical to the first one, then the data has not been altered. Hash values are similar to 'file fingerprints' and are used to ensure data integrity.

The HASH function included with DBMS_CRYPTO, is a one-way hash function that you can use to generate a hash value from either RAW or LOB data. The MAC function is also a one-way hash function, but with the addition of a secret key. It works the same way as the DBMS_CRYPTO.HASH function, except only someone with the key can verify the hash value.

MACs can be used to authenticate files between users. They can also be used by a single user to determine if her files have been altered, perhaps by a virus. A user could compute the MAC of his files and store that value in a table. If the user did not use a MAC function, then the virus could compute the new hash value after infection and replace the table entry. A virus cannot do that with a MAC because the virus does not know the key.

About Generating and Storing Encryption Keys

The DBMS_CRYPTO package can generate random material for encryption keys, but it does not provide a mechanism for maintaining them. Application developers must take care to ensure that the encryption keys used with this package are securely generated and stored. Also note that the encryption and decryption operations performed by DBMS_CRYPTO occur on the server, not on the client. Consequently, if the key is sent over the connection between the client and the server, the connection must be protected by using network encryption. Otherwise, the key is vulnerable to capture over the wire.

Although DBMS_CRYPTO cannot generate keys on its own, it does provide tools you can use to aid in key generation. For example, you can use the RANDOMBYTES function to generate random material for keys.

When generating encryption keys for DES, it is important to remember that some numbers are considered weak and semiweak keys. Keys are considered weak or semiweak when the pattern of the algorithm combines with the pattern of the initial key value to produce ciphertext that is more susceptible to cryptanalysis. To avoid this, filter out the known weak DES keys. Lists of the known weak and semiweak DES keys are available on several public Internet sites.

Conversion Rules

To convert VARCHAR2 to RAW, use the UTL_I18N.STRING_TO_RAW function to perform the following steps:
1. Convert VARCHAR2 in the current database character set to VARCHAR2 in the AL32UTF8 database character.
2. Convert VARCHAR2 in the AL32UTF8 database character set to RAW.
Syntax example:
To convert RAW to VARCHAR2, use the UTL_I18N.RAW_TO_CHAR function to perform the following steps:
1. Convert RAW to VARCHAR2 in the AL32UTF8 database character set.
2. Convert VARCHAR2 in the AL32UTF8 database character set to VARCHAR2 in the database character set you wish to use.
Syntax example:
See Also:
Chapter 253, 'UTL_I18N' for information about using the UTL_I18N PL/SQL package.
If you want to store encrypted data of the RAW datatype in a VARCHAR2 database column, then use RAWTOHEX or UTL_ENCODE.BASE64_ENCODE to make it suitable for VARCHAR2 storage. These functions expand data size by 2 and 4/3, respectively.

Examples

The following listing shows PL/SQL block encrypting and decrypting pre-defined 'input_string' using 256-bit AES algorithm with Cipher Block Chaining and PKCS#5 compliant padding.

Hash Generation Requires Secret Key West

Summary of DBMS_CRYPTO Subprograms

Table 40-10 DBMS_CRYPTO Package Subprograms

Subprogram	Description
Decrypts `RAW` data using a stream or block cipher with a user supplied key and optional IV (initialization vector)
Decrypts `LOB` data using a stream or block cipher with a user supplied key and optional IV
Encrypts `RAW` data using a stream or block cipher with a user supplied key and optional IV
Encrypts `LOB` data using a stream or block cipher with a user supplied key and optional IV
Applies one of the supported cryptographic hash algorithms (MD4, MD5, SHA-1, or SHA-2) to data
Applies Message Authentication Code algorithms (MD5, SHA-1, or SHA-2) to data to provide keyed message protection
Returns a `RAW` value containing a cryptographically secure pseudo-random sequence of bytes, and can be used to generate random material for encryption keys
Returns a random `BINARY_INTEGER`
Returns a random 128-bit integer of the `NUMBER` datatype

DECRYPT Function

This function decrypts RAW data using a stream or block cipher with a user supplied key and optional IV (initialization vector).

Pragmas

Parameters

Table 40-11 DECRYPT Function Parameters

Parameter Name	Description
`src`	`RAW` data to be decrypted.
`typ`	Stream or block cipher type and modifiers to be used.
`key`	Key to be used for decryption.
`iv`	Optional initialization vector for block ciphers. Default is `NULL`.

Usage Notes

To retrieve original plaintext data, DECRYPT must be called with the same cipher, modifiers, key, and IV that was used to encrypt the data originally.
See Also:
'Usage Notes' for the ENCRYPT function for additional information about the ciphers and modifiers available with this package.
If VARCHAR2 data is converted to RAW before encryption, then it must be converted back to the appropriate database character set by using the UTL_I18N package.
See Also:
'Conversion Rules' for a discussion of the VARCHAR2 to RAW conversion process.

DECRYPT Procedures

These procedures decrypt LOB data using a stream or block cipher with a user supplied key and optional IV (initialization vector).

Pragmas

Parameters

Table 40-12 DECRYPT Procedure Parameters

Parameter Name	Description
dst	`LOB` locator of output data. The value in the output `LOB` <`dst`> will be overwritten.
`src`	`LOB` locator of input data.
`typ`	Stream or block cipher type and modifiers to be used.
`key`	Key to be used for decryption.
`iv`	Optional initialization vector for block ciphers. Default is all zeroes.

ENCRYPT Function

This function encrypts RAW data using a stream or block cipher with a user supplied key and optional IV (initialization vector).

Pragmas

Parameters

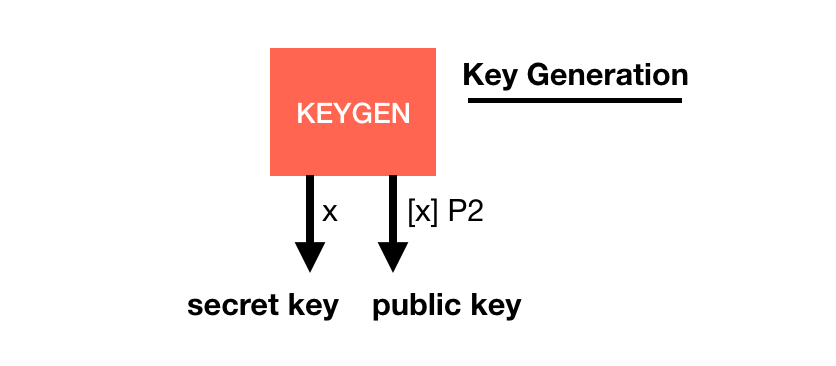
Table 40-13 ENCRYPT Function Parameters

Parameter Name	Description
`src`	`RAW` data to be encrypted.
`typ`	Stream or block cipher type and modifiers to be used.
`key`	Encryption key to be used for encrypting data.
`iv`	Optional initialization vector for block ciphers. Default is `NULL`.

Usage Notes

Block ciphers may be modified with chaining and padding type modifiers. The chaining and padding type modifiers are added to the block cipher to produce a cipher suite. Cipher Block Chaining (CBC) is the most commonly used chaining type, and PKCS #5 is the recommended padding type. See Table 40-7 and Table 40-8 for block cipher chaining and padding modifier constants that have been defined for this package.
To improve readability, you can define your own package-level constants to represent the cipher suites you use for encryption and decryption. For example, the following example defines a cipher suite that uses DES, cipher block chaining mode, and no padding:
See Table 40-6 for the block cipher suites already defined as constants for this package.
To encrypt VARCHAR2 data, it should first be converted to the AL32UTF8 character set.
See Also:
'Conversion Rules' for a discussion of the conversion process.
Stream ciphers, such as RC4, are not recommended for stored data encryption.

ENCRYPT Procedures

These procedures encrypt LOB data using a stream or block cipher with a user supplied key and optional IV (initialization vector).

Pragmas

Parameters

Table 40-14 ENCRYPT Procedure Parameters

Parameter Name	Description
dst	`LOB` locator of output data. The value in the output `LOB` <`dst`> will be overwritten.
`src`	`LOB` locator of input data.
`typ`	Stream or block cipher type and modifiers to be used.
`key`	Encryption key to be used for encrypting data.
`iv`	Optional initialization vector for block ciphers. Default is `NULL`.

Usage Notes

See 'Conversion Rules' for usage notes about using the ENCRYPT procedure.

HASH Function

A one-way hash function takes a variable-length input string, the data, and converts it to a fixed-length (generally smaller) output string called a hash value. The hash value serves as a unique identifier (like a fingerprint) of the input data. You can use the hash value to verify whether data has been changed or not.

Note that a one-way hash function is a hash function that works in one direction. It is easy to compute a hash value from the input data, but it is hard to generate data that hashes to a particular value. Consequently, one-way hash functions work well to ensure data integrity. Refer to 'When to Use Hash or Message Authentication Code (MAC) Functions' for more information about using one-way hash functions.

This function applies to data one of the supported cryptographic hash algorithms listed in Table 40-3.

Pragmas

Parameters

Table 40-15 HASH Function Parameters

Parameter Name	Description
`src`	The source data to be hashed.
`typ`	The hash algorithm to be used.

Usage Note

Oracle recommends that you use the SHA-1 (Secure Hash Algorithm) or SHA-2 because it is more resistant to brute-force attacks than MD4 or MD5. If you must use a Message Digest algorithm, then MD5 provides greater security than MD4.

MAC Function

A Message Authentication Code, or MAC, is a key-dependent one-way hash function. MACs have the same properties as the one-way hash function described in 'HASH Function', but they also include a key. Only someone with the identical key can verify the hash. Also refer to 'When to Use Hash or Message Authentication Code (MAC) Functions' for more information about using MACs.

This function applies MAC algorithms to data to provide keyed message protection. See Table 40-4 for a list of MAC algorithms that have been defined for this package.

Pragmas

Parameters

Table 40-16 MAC Function Parameters

Parameter Name	Description
`src`	Source data to which MAC algorithms are to be applied.
`typ`	MAC algorithm to be used.
`key`	Key to be used for MAC algorithm.

RANDOMBYTES Function

This function returns a RAW value containing a cryptographically secure pseudo-random sequence of bytes, which can be used to generate random material for encryption keys. The RANDOMBYTES function is based on the RSA X9.31 PRNG (Pseudo-Random Number Generator).

Pragmas

Parameters

Table 40-17 RANDOMBYTES Function Parameter

Parameter Name	Description
`number_bytes`	The number of pseudo-random bytes to be generated.

Usage Note

The number_bytes value should not exceed the maximum length of a RAW variable.

RANDOMINTEGER Function

This function returns an integer in the complete range available for the Oracle BINARY_INTEGER datatype.

Pragmas

RANDOMNUMBER Function

This function returns an integer in the Oracle NUMBER datatype in the range of [0.2**128-1].

Pragmas

Hash-based cryptography is the generic term for constructions of cryptographic primitives based on the security of hash functions. It is of interest as a type of post-quantum cryptography.

So far, hash-based cryptography is limited to digital signatures schemes such as the Merkle signature scheme. Hash-based signature schemes combine a one-time signature scheme with a Merkle tree structure. Since a one-time signature scheme key can only sign a single message securely, it is practical to combine many such keys within a single, larger structure. A Merkle tree structure is used to this end. In this hierarchical data structure, a hash function and concatenation are used repeatedly to compute tree nodes. Lamport signatures are an example of a one-time signature scheme that can be combined with a Merkle tree structure.

In 2019, the US National Institute of Standards and Technology announced its intention to promulgate standards for stateful hash-based cryptography based on the eXtended Merkle Signature Scheme (XMSS) and Leighton-Micali Signatures (LMS), which are applicable in different circumstances.^[1]

History[edit]

Leslie Lamport invented hash-based signatures in 1979. The XMSS (eXtended Merkle Signature Scheme)^[2] and SPHINCS^[3]^[4] hash-based signature schemes were introduced in 2011 and 2015, respectively. XMSS was developed by a team of researchers under the direction of Johannes Buchmann and is based both on Merkle's seminal scheme and on the 2007 Generalized Merkle Signature Scheme (GMSS)^[5]. A multi-tree variant of XMSS, XMSS^MT, was described in 2013.^[6]

One-time signature schemes[edit]

Hash-based signature schemes use one-time signature schemes as their building block. A given one-time signing key can only be used to sign a single message securely. Indeed, signatures reveal part of the signing key. The security of (hash-based) one-time signature schemes relies exclusively on the security of an underlying hash function.

Commonly used one-time signature schemes include the Lamport-Diffie scheme, the Winternitz scheme^[7] and its improvements, such as the W-OTS⁺ scheme^[8]. Unlike the seminal Lamport-Diffie scheme, the Winternitz scheme and variants can sign many bits at once. The number of bits to be signed at once is determined by a value: the Winternitz parameter. The existence of this parameter provides a trade-off between size and speed. Large values of the Winternitz parameter yield short signatures and keys, at the price of slower signing and verifying. In practice, a typical value for this parameter is 16.

In the case of stateless hash-based signatures, few-time signature schemes are used. Such schemes allow security to decrease gradually in case a few-time key is used more than once. HORST is an example of a few-time signature scheme.

Combining many one-time key pairs into a hash-based signature scheme[edit]

The central idea of hash-based signature schemes is to combine a larger number of one-time key pairs into a single structure to obtain a practical way of signing more than once (yet a limited number of times). This is done using a Merkle tree structure, with possible variations. One public and one private key are constructed from the numerous public and private keys of the underlying one-time scheme. The global public key is the single node at the very top of the Merkle tree. Its value is an output of the selected hash function, so a typical public key size is 32 bytes. The validity of this global public key is related to the validity of a given one-time public key using a sequence of tree nodes. This sequence is called the authentication path. It is stored as part of the signature, and allows a verifier to reconstruct the node path between those two public keys.

The global private key is generally handled using a pseudo-random number generator. It is then sufficient to store a seed value. One-time secret keys are derived successively from the seed value using the generator. With this approach, the global private key is also very small, e.g. typically 32 bytes.

The problem of tree traversal is critical to signing performance. Increasingly efficient approaches have been introduced, dramatically speeding up signing time.

Some hash-based signature schemes use multiple layers of tree, offering faster signing at the price of larger signatures. In such schemes, only the lowest layer of trees is used to sign messages, while all other trees sign root values of lower trees.

The Naor-Yung work^[9] shows the pattern by which to transfer a limited time signature of the Merkle type family into an unlimited (regular) signature scheme.

Properties of hash-based signature schemes[edit]

Hash-based signature schemes rely on security assumptions about the underlying hash function, but any hash function fulfilling these assumptions can be used. As a consequence, each adequate hash function yields a different corresponding hash-based signature scheme. Even if a given hash function becomes insecure, it is sufficient to replace it by a different, secure one to obtain a secure instantiation of the hash-based signature scheme under consideration. Some hash-based signature schemes (such as XMSS with pseudorandom key generation) are forward secure, meaning that previous signatures remain valid if a secret key is compromised.

The minimality of security assumptions is another characteristic of hash-based signature schemes. Generally, these schemes only require a secure (for instance in the sense of second preimage resistance) cryptographic hash function to guarantee the overall security of the scheme. This kind of assumption is necessary for any digital signature scheme; however, other signature schemes require additional security assumptions, which is not the case here.

Because of their reliance on an underlying one-time signature scheme, hash-based signature schemes can only sign a fixed number of messages securely. In the case of the Merkle and XMSS schemes, a maximum of ${displaystyle 2^{h}}$ messages can be signed securely, with ${displaystyle h}$ the total Merkle tree height.

Examples of hash-based signature schemes[edit]

Since Merkle's initial scheme, numerous hash-based signature schemes with performance improvements have been introduced. Recent ones include the XMSS, the Leighton-Micali (LMS), the SPHINCS and the BPQS schemes. Most hash-based signature schemes are stateful, meaning that signing requires updating the secret key, unlike conventional digital signature schemes. For stateful hash-based signature schemes, signing requires keeping state of the used one-time keys and making sure they are never reused. The XMSS, LMS and BPQS^[10] schemes are stateful, while the SPHINCS scheme is stateless. SPHINCS signatures are larger than XMSS, LMS signatures, while BPQS has been designed specifically for blockchain systems. Additionally to the WOTS⁺ one-time signature scheme^[8], SPHINCS also uses a few-time (hash-based) signature scheme called HORST. HORST is an improvement of an older few-time signature scheme, HORS (Hash to Obtain Random Subset).^[11]

The stateful hash-based schemes XMSS and XMSS^MT are specified in RFC 8391 (XMSS: eXtended Merkle Signature Scheme)^[12].Leighton-Micali Hash-Based Signatures are specified in RFC 8554.^[13] Practical improvements have been proposed in the literature that alleviate the concerns introduced by stateful schemes.^[14] Hash functions appropriate for these schemes include SHA-2, SHA-3 and BLAKE.

Implementations[edit]

Unlike other popular blockchain networks and cryptocurrencies that use already NIST standardized Elliptic Curve Digital Signature Algorithms (ECDSA)^[15], The Quantum Resistant Ledger (QRL) is the first open source network to implement eXtended Merkle Signature Scheme^[16]. In contrast to traditional ECDSA signatures, this stateful signature scheme is provably resistant to a sufficiently powerful quantum computer running Shor’s algorithm.^[17]^[18]

The XMSS, GMSS and SPHINCS schemes are available in the Java Bouncy Castle cryptographic APIs.^[19] SPHINCS is implemented in the SUPERCOP benchmarking toolkit.^[20] Optimised^[21] and unoptimised^[22] reference implementations of the XMSS RFC exist. The LMS scheme has been implemented in Python^[23] and in C^[24] following its Internet-Draft.

References[edit]

^Computer Security Division, Information Technology Laboratory (2019-02-01). 'Request for Public Comments on Stateful HBS CSRC'. CSRC NIST. Retrieved 2019-02-04.
^Buchmann, Johannes; Dahmen, Erik; Hülsing, Andreas (2011). 'XMSS - A Practical Forward Secure Signature Scheme Based on Minimal Security Assumptions'. Lecture Notes in Computer Science. 7071 (Post-Quantum Cryptography. PQCrypto 2011): 117–129. CiteSeerX10.1.1.400.6086. doi:10.1007/978-3-642-25405-5_8. ISSN0302-9743.
^Bernstein, Daniel J.; Hopwood, Daira; Hülsing, Andreas; Lange, Tanja; Niederhagen, Ruben; Papachristodoulou, Louiza; Schneider, Michael; Schwabe, Peter; Wilcox-O’Hearn, Zooko (2015). Oswald, Elisabeth; Fischlin, Marc (eds.). SPHINCS: practical stateless hash-based signatures. Lecture Notes in Computer Science. 9056. Springer Berlin Heidelberg. pp. 368–397. CiteSeerX10.1.1.690.6403. doi:10.1007/978-3-662-46800-5_15. ISBN9783662467992.
^'SPHINCS: Introduction'.
^Buchmann, Johannes; Dahmen, Erik; Klintsevich, Elena; Okeya, Katsuyuki; Vuillaume, Camille (2007). 'Merkle Signatures with Virtually Unlimited Signature Capacity'. Lecture Notes in Computer Science. 4521 (Applied Cryptography and Network Security): 31–45. doi:10.1007/978-3-540-72738-5_3.
^Hülsing, Andreas; Rausch, Lea; Buchmann, Johannes (2013). Optimal Parameters for XMSSMT. Lecture Notes in Computer Science. 8128. p. 194–208. doi:10.1007/978-3-642-40588-4_14. ISBN978-3-642-40587-7.
^Dods, C.; Smart, N. P.; Stam, M. (2005). 'Hash Based Digital Signature Schemes'. Lecture Notes in Computer Science. 3796 (Cryptography and Coding): 96–115. doi:10.1007/11586821_8.
^ ^a^bHülsing, Andreas (2013). W-OTS+ — Shorter Signatures for Hash-Based Signature Schemes. Lecture Notes in Computer Science. 7918. pp. 173–188. doi:10.1007/978-3-642-38553-7_10. ISBN978-3-642-38552-0.
^M. Naor, M. Yung. 'Universal One-Way Hash Functions and their Cryptographic Applications'. STOC 1989. [1]
^Chalkias, Konstantinos; Brown, James; Hearn, Mike; Lillehagen, Tommy; Nitto, Igor; Schroeter, Thomas (2018). 'Blockchained Post-Quantum Signatures'(PDF). Proceedings of the IEEE International Conference on Blockchain (Cybermatics-2018): 1196–1203.
^Reyzin, Leonid; Reyzin, Natan (2002). Better than BiBa: Short One-Time Signatures with Fast Signing and Verifying. Lecture Notes in Computer Science. 2384. p. 144–153. CiteSeerX10.1.1.24.7320. doi:10.1007/3-540-45450-0_11. ISBN978-3-540-43861-8.
^Hülsing, Andreas; Butin, Denis; Gazdag, Stefan; Rijneveld, Joost; Mohaisen, Aziz. 'RFC 8391 - XMSS: eXtended Merkle Signature Scheme'. tools.ietf.org. IETF.
^McGrew, David; Curcio, Michael; Fluhrer, Scott. 'RFC 8554 - Leighton-Micali Hash-Based Signatures'. tools.ietf.org. IETF.
^McGrew, David; Kampanakis, Panos; Fluhrer, Scott; Gazdag, Stefan-Lukas; Butin, Denis; Buchmann, Johannes (2016). 'State Management for Hash-Based Signatures'(PDF). Lecture Notes in Computer Science. 10074 (Security Standardisation Research): 244–260. doi:10.1007/978-3-319-49100-4_11.
^Wang, Licheng; Shen, Xiaoying; Li, Jing; Shao, Jun; Yang, Yixian (2019-02-01). 'Cryptographic primitives in blockchains'. Journal of Network and Computer Applications. 127: 43–58. doi:10.1016/j.jnca.2018.11.003. ISSN1084-8045.
^'The Quantum Resistant Ledger'. theqrl.org. 2019-08-24.
^'NIST Stateful Hash-Based Signatures'(PDF). NIST. 2019-02-04.
^Computer Security Division, Information Technology Laboratory (2018-12-20). 'Hash-Based Signatures CSRC'. CSRC NIST. Retrieved 2019-09-06.
^'bcgit/bc-java'. GitHub. 2018-12-18.
^'SUPERCOP'. Archived from the original on 2015-02-15. Retrieved 2017-05-31.
^'Code'. Andreas Hülsing.
^'squareUP > Publications'. www.pqsignatures.org.
^David, McGrew (2018-05-29). 'The hash-sigs package: an implementation of the Leighton-Micali Hierarchical Signature System (HSS)'. GitHub.
^David, McGrew (2018-11-22). 'A full-featured implementation of the LMS and HSS Hash Based Signature Schemes from draft-mcgrew-hash-sigs-07'. GitHub.

T. Lange. 'Hash-Based Signatures'. Encyclopedia of Cryptography and Security, Springer US, 2011. [2]
F. T. Leighton, S. Micali. 'Large provably fast and secure digital signature schemes based one secure hash functions'. US Patent 5,432,852, [3] 1995.
G. Becker. 'Merkle Signature Schemes, Merkle Trees and Their Cryptanalysis', seminar 'Post Quantum Cryptology' at the Ruhr-University Bochum, Germany, 2008. [4]
E. Dahmen, M. Dring, E. Klintsevich, J. Buchmann, L.C. Coronado Garcia. 'CMSS — An Improved Merkle Signature Scheme'. Progress in Cryptology - Indocrypt 2006. [5]
R. Merkle. 'Secrecy, authentication and public key systems / A certified digital signature'. Ph.D. dissertation, Dept. of Electrical Engineering, Stanford University, 1979. [6]
S. Micali, M. Jakobsson, T. Leighton, M. Szydlo. 'Fractal Merkle Tree Representation and Traversal'. RSA-CT 03. [7]
P. Kampanakis, S. Fluhrer. 'LMS vs XMSS: A comparison of the Stateful Hash-Based Signature Proposed Standards'. Cryptology ePrint Archive, Report 2017/349. [8]
D. Naor, A. Shenhav, A. Wool. 'One-Time Signatures Revisited: Practical Fast Signatures Using Fractal Merkle Tree Traversal'. IEEE 24th Convention of Electrical and Electronics Engineers in Israel, 2006. [9]

Hash Generation Requires Secret Key Movie

External links[edit]

[10] A commented list of literature about hash-based signature schemes.
[11] Another list of references (uncommented).

Retrieved from 'https://en.wikipedia.org/w/index.php?title=Hash-based_cryptography&oldid=942870407'

ntv.netlify.com

Hash Generation Requires Secret Key

Using the DBMS_CRYPTO Subprograms

Overview

Security Model

Datatypes

Algorithms

Restrictions

Exceptions

Operational Notes

When to Use Encrypt and Decrypt Procedures or Functions

When to Use Hash or Message Authentication Code (MAC) Functions

About Generating and Storing Encryption Keys

Conversion Rules

Examples

Hash Generation Requires Secret Key West

Summary of DBMS_CRYPTO Subprograms

DECRYPT Function

DECRYPT Procedures

ENCRYPT Function

ENCRYPT Procedures

HASH Function

MAC Function

RANDOMBYTES Function

RANDOMINTEGER Function

RANDOMNUMBER Function

History[edit]

One-time signature schemes[edit]

Combining many one-time key pairs into a hash-based signature scheme[edit]

Properties of hash-based signature schemes[edit]

Examples of hash-based signature schemes[edit]

Implementations[edit]

References[edit]

Hash Generation Requires Secret Key Movie

External links[edit]

Top Posts